[এই অধ্যায়ের প্রয়োজনীয় পূর্বজ্ঞান বইয়ের শেষে পরিশিষ্ট অংশে সংযুক্ত আছে। প্রথমে পরিশিষ্ট অংশ পাঠ/আলোচনা করতে হবে।]

বৈচিত্র্যময় প্রকৃতির এই বৈচিত্র্য আমরা গণনা ও সংখ্যার সাহায্যে উপলব্ধি করি। পূর্ববর্তী শ্রেণিতে আমরা স্বাভাবিক সংখ্যা, পূর্ণসংখ্যা ও ভগ্নাংশ সম্পর্কে ধারণা পেয়েছি যা মূলদ সংখ্যা হিসেবে পরিচিত। এ সংখ্যাগুলোকে দুটি পূর্ণসংখ্যার অনুপাতে প্রকাশ করা যায়। সংখ্যাজগতে কিছু সংখ্যা রয়েছে যেগুলো দুটি পূর্ণসংখ্যার অনুপাতে প্রকাশ করা যায় না। এগুলো অমূলদ সংখ্যা নামে পরিচিত। এ অধ্যায়ে আমরা অমূলদ সংখ্যার সাথে পরিচিত হয়ে এদের প্রয়োগ সম্পর্কে আলোচনা করব।

অধ্যায় শেষে শিক্ষার্থীরা-

• সংখ্যার বর্গ ও বর্গমূল ব্যাখ্যা করতে পারবে।
• উৎপাদক ও ভাগ প্রক্রিয়ার মাধ্যমে বর্গমূল নির্ণয় করতে পারবে।
• সংখ্যার বর্গমূল নির্ণয় পদ্ধতিগুলো প্রয়োগ করে বাস্তব জীবনে সমস্যার সমাধান করতে পারবে।
• মূলদ ও অমূলদ সংখ্যা শনাক্ত করতে পারবে।
• সংখ্যারেখায় মূলদ ও অমূলদ সংখ্যার অবস্থান দেখাতে পারবে।

বর্গ একটি আয়ত, যার বাহুগুলো পরস্পর সমান। বর্গের বাহুর দৈর্ঘ্য 'ক' একক হলে বর্গক্ষেত্রের ক্ষেত্রফল হবে (কক) বর্গ একক বা ক' বর্গ একক।
বিপরীতভাবে, বর্গক্ষেত্রের ক্ষেত্রফল ক' বর্গ একক হলে, এর প্রতিটি বাহুর দৈর্ঘ্য হবে 'ক' একক।

চিত্রে, ৯টি মার্বেলকে বর্গাকারে সাজানো হয়েছে। সমান দূরত্বে প্রতিটি সারিতে ৩টি করে ৩টি সারিতে মার্বেল সাজানো আছে এবং মোট মার্বেলের সংখ্যা ৩ × ৩ = ৩ = ৯। এখানে, প্রত্যেক সারিতে মার্বেলের সংখ্যা এবং সারির সংখ্যা সমান। তাই চিত্রটি বর্গাকৃতির হয়েছে। ফলে ৩ এর বর্গ ৯ এবং ৯ এর বর্গমূল ৩।

কোনো সংখ্যাকে সেই সংখ্যা দ্বারা গুণ করলে যে গুণফল পাওয়া যায় তা ঐ সংখ্যার বর্গ এবং সংখ্যাটি গুণফলের বর্গমূল।

নিচের সারণিটি লক্ষ করি:

১, ৪, ৯, ২৫, ৪৯ সংখ্যাগুলোর বৈশিষ্ট্য হলো যে, এগুলোকে অন্য কোনো পূর্ণসংখ্যার বর্গ হিসেবে প্রকাশ করা যায়। ১, ৪, ৯, ২৫, ৪৯ সংখ্যাগুলো পূর্ণ বর্গসংখ্যা।

পূর্ণবর্গ সংখ্যার বর্গমূল একটি স্বাভাবিক সংখ্যা।
যেমন: ২১ এর বর্গ ২১^২ বা ৪৪১ একটি পূর্ণবর্গ সংখ্যা এবং ৪৪১ এর বর্গমূল ২১ একটি স্বাভাবিক সংখ্যা।

বর্গসংখ্যার ধর্ম

নিচের সারণিতে ১ থেকে ২০ সংখ্যার বর্গসংখ্যা দেওয়া হয়েছে। খালি ঘরগুলো পূরণ কর।

সারণিভুক্ত বর্গসংখ্যাগুলোর এককের ঘরের অঙ্কগুলো ভালোভাবে পর্যবেক্ষণ করি। লক্ষ করি যে, এ সংখ্যাগুলোর একক স্থানীয় অঙ্ক ০, ১,৪, ৫, ৬ বা ৯। কোনো বর্গসংখ্যার একক স্থানে ২, ৩, ৭, বা ৮ অঙ্কটি নেই।

এবার সারণি থেকে একক স্থানে ১ রয়েছে এমন বর্গসংখ্যা নিই।

একইভাবে

এবং

• যে সংখ্যার সর্ব ডানদিকের অঙ্ক অর্থাৎ একক স্থানীয় অঙ্ক ২ বা ৩ বা ৭ বা ৮ তা পূর্ণবর্গ নয়।
• যে সংখ্যার শেষে বিজোড় সংখ্যক শূন্য থাকে, ঐ সংখ্যা পূর্ণবর্গ নয়।
• একক স্থানীয় অঙ্ক ১ বা ৪ বা ৫ বা ৬ বা ৯ হলে, ঐ সংখ্যা পূর্ণবর্গ হতে পারে। যেমন: ৮১, ৬৪, ২৫, ৩৬, ৪৯ ইত্যাদি বর্গসংখ্যা।
• আবার সংখ্যার ডানদিকে জোড়সংখ্যক শূন্য থাকলে ঐ সংখ্যা পূর্ণবর্গ হতে পারে। যেমন: ১০০, ৪৯০০ ইত্যাদি বর্গসংখ্যা।

নিচে বর্গমূলসহ কয়েকটি পূর্ণ বর্গসংখ্যার তালিকা দেওয়া হলো:

বর্গমূলের চিহ্ন

বর্গমূল প্রকাশের জন্য $\sqrt{}$ চিহ্ন ব্যবহৃত হয়। ২৫ এর বর্গমূল বোঝাতে লেখা হয় $\sqrt{২৫}$ আমরা জানি, ৫ $\times$ ৫ = ২৫, কাজেই ২৫ এর বর্গমূল ৫।

মৌলিক গুণনীয়কের সাহায্যে বর্গমূল নির্ণয়

১৬ কে মৌলিক গুণনীয়কে বিশ্লেষণ করে পাই

১৬ = ২$\times$২$\times$২$\times$২= (২ $\times$ ২) $\times$ (২$\times$২)

প্রতি জোড়া থেকে একটি করে গুণনীয়ক নিয়ে পাই ২ $\times$ ২ = ৪

$\therefore$ ১৬ এর বর্গমূল = $\sqrt{১৬}$ = ৪

আবার, ৩৬ কে মৌলিক গুণনীয়কে বিশ্লেষণ করে পাই,

$৩৬ = ২ \times ২ \times ৩ \times ৩ = (২ \times ২) \times (৩ \times ৩)$

প্রতি জোড়া থেকে একটি করে গুণনীয়ক নিয়ে পাই ২ $\times$ ৩ = ৬

৩৬ এর বর্গমূল = $\sqrt{৩৬}$ = ৬

লক্ষ করি: মৌলিক গুণনীয়কের সাহায্যে কোনো পূর্ণ বর্গসংখ্যার বর্গমূল নির্ণয় করার সময় -

• প্রথমে প্রদত্ত সংখ্যাটিকে মৌলিক গুণনীয়কে বিশ্লেষণ করতে হবে।
• প্রতি জোড়া একই গুণনীয়ককে একসাথে পাশাপাশি লিখতে হবে।
• প্রতি জোড়া এক জাতীয় গুণনীয়কের পরিবর্তে একটি গুণনীয়ক নিয়ে লিখতে হবে।
• প্রাপ্ত গুণনীয়কগুলোর ধারাবাহিক গুণফল হবে নির্ণেয় বর্গমূল।

উদাহরণ ১। ৩১৩৬ এর বর্গমূল নির্ণয় কর।

সমাধান:

এখানে,

$৩১৩৬ = ২\times ২\times ২\times ২\times ২\times ২\times ৭\times ৭$

$= (২ \times ২) \times (২ \times ২) \times (২\times ২) \times (৭ \times ৭)$

৩১৩৬ এর বর্গমূল = $\sqrt{৩১৩৬}$ $= ২\times ২\times ২\times ৭ = ৫৬$

একটি উদাহরণ দিয়ে ভাগের সাহায্যে বর্গমূল নির্ণয়ের পদ্ধতি দেখানো হলো:

উদাহরণ ২। ভাগের সাহায্যে ২৩০৪ এর বর্গমূল নির্ণয় কর:

সমাধান

(১) ২৩০৪ সংখ্যাটি লিখি

(২) ডানদিক থেকে দুটি করে অঙ্ক নিয়ে জোড়া করি। প্রত্যেক জোড়ার উপর রেখাচিহ্ন দিই:

(৩) ভাগের সময় যেমন খাড়া দাগ দেওয়া হয়, ডানপাশে তদ্রূপ একটি খাড়া দাগ দিই:

(৪) প্রথম জোড়াটি ২৩। এর পূর্ববর্তী বর্গসংখ্যাটি ১৬, যার বর্গমূল $\sqrt{১৬}$ বা ৪; খাড়া দাগের ডানপাশে ৪ লিখি। এখন ২৩ এর ঠিক নিচে ১৬ লিখি:

(৫) এখন ২৩ থেকে ১৬ বিয়োগ করি:

(৬) বিয়োগফল ৭ এর ডানে পরবর্তী জোড়া ০৪ বসাই। ৭০৪ এর বামদিকে খাড়া দাগ (ভাগের চিহ্ন) দিই:

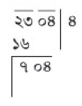
(৭) ভাগফলের ঘরের সংখ্যা ৪ এর দ্বিগুণ ৪ × ২ বা ৮ নিচের খাড়া দাগের বামপাশে বসাই। ৮ এবং খাড়া দাগের মধ্যে একটি অঙ্ক বসানোর মতো স্থান রাখি:

(৮) এখন একটি এক অঙ্কের সংখ্যা খুঁজে বের করি যাকে ৮ এর ডানপাশে বসিয়ে প্রাপ্ত সংখ্যাকে ঐ সংখ্যাটি দ্বারা গুণ করে ৭০৪ এর সমান বা অনূর্ধ্ব ৭০৪ পাওয়া যায়। এক্ষেত্রে ৮ হবে। ৮ সংখ্যাটি ভাগফলেও ৪ এর ডানপাশে বসাই।

(৯) ভাগফলের স্থানে পাওয়া গেল ৪৮। এটিই নির্ণেয় বর্গমূল।

$\therefore$ $\sqrt{২৩০৪ }=৪৮$

লক্ষণীয় যে ভাগের সাহায্যে বর্গমূল নির্ণয় করার সময় সংখ্যার ডান দিক থেকে জোড় করতে গিয়ে শেষ অঙ্কের জোড় না থাকলে একে জোড়া ছাড়াই গণ্য করতে হবে।

উদাহরণ ৩। ভাগের সাহায্যে ৩১৬৮৪ এর বর্গমূল নির্ণয় কর।

সমাধান:

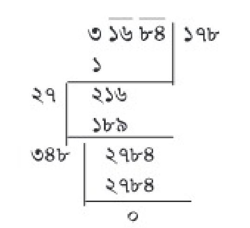
$\therefore$ ৩১৬৮৪ এর বর্গমূল = $\sqrt{৩১৬৮৪}$ = ১৭৮

নির্ণেয় বর্গমূল ১৭৮।

বর্গসংখ্যা ও বর্গমূল সম্বন্ধে উল্লেখ্য বিষয়

• কোনো সংখ্যার একক স্থানীয় অঙ্ক থেকে শুরু করে বামদিকে এক অঙ্ক পরপর যতটি ফোঁটা দেওয়া যায়, এর বর্গমূলের সংখ্যাটি তত অঙ্কবিশিষ্ট।

লক্ষণীয় যে

$\sqrt{৮১ }= ৯$ (এক অঙ্কবিশিষ্ট, এখানে ফোঁটার সংখ্যা ১ কারণ, ৮১)

$\sqrt{১০০} = ১০$ (দুই অঙ্কবিশিষ্ট, এখানে ফোঁটার সংখ্যা ২ কারণ, ১০০)

$\sqrt{৪৭০৮৯} = ২১৭$ (তিন অঙ্কবিশিষ্ট, এখানে ফোঁটার সংখ্যা ৩ কারণ, ৪৭০৮৯)

বর্গ ও বর্গমূল সংশ্লিষ্ট সমস্যা

উদাহরণ ৪। ৮৬৫৫ থেকে কোন ক্ষুদ্রতম সংখ্যা বিয়োগ করলে বিয়োগফল একটি পূর্ণ বর্গসংখ্যা হবে?

সমাধান:

এখানে, ৮৬৫৫ এর বর্গমূল ভাগের সাহায্যে নির্ণয় করতে গিয়ে ৬ অবশিষ্ট থাকে।
সুতরাং প্রদত্ত সংখ্যা থেকে ৬ বাদ দিলে প্রাপ্ত সংখ্যাটি পূর্ণ বর্গসংখ্যা হবে।
নির্ণেয় ক্ষুদ্রতম সংখ্যা ৬

উদাহরণ ৫। ৬৫১২০১ এর সাথে কোন ক্ষুদ্রতম সংখ্যা যোগ করলে যোগফল একটি পূর্ণ বর্গসংখ্যা হবে?

সমাধান:

যেহেতু সংখ্যাটির বর্গমূল নির্ণয় করার সময় ভাগশেষ ১৫৬৫ আছে। কাজেই প্রদত্ত সংখ্যাটি পূর্ণ বর্গসংখ্যা নয়। ৬৫১২০১ এর সাথে কোনো ক্ষুদ্রতম সংখ্যা যোগ করলে যোগফল পূর্ণবর্গ হবে এবং তখন এর বর্গমূল হবে

৮০৬ + ১ = ৮০৭
৮০৭ এর বর্গ = ৮০৭ $\times$ ৮০৭ = ৬৫১২৪৯

নির্ণেয় ক্ষুদ্রতম সংখ্যাটি = ৬৫১২৪৯ ৬৫১২০১

= ৪৮

১। মৌলিক গুণনীয়কের সাহায্যে বর্গমূল নির্ণয় কর:

(ক) ১৬৯
(খ) ৫২৯
(গ) ১৫২১
(ঘ) ১১০২৫

২। ভাগের সাহায্যে বর্গমূল নির্ণয় কর:

(ক) ২২৫
(খ) ৯৬১
(গ) ৩৯৬৯
(ঘ) ১০৪০৪

৩। নিচের সংখ্যাগুলোকে কোন ক্ষুদ্রতম সংখ্যা দ্বারা গুণ করলে গুণফল পূর্ণবর্গ সংখ্যা হবে?

(ক) ১৪৭
(খ) ৩৮৪
(গ) ১৪৭০
(ঘ) ২৩৮০৫

8। নিচের সংখ্যাগুলোকে কোন ক্ষুদ্রতম সংখ্যা দ্বারা ভাগ করলে ভাগফল পূর্ণবর্গ সংখ্যা হবে?

(ক) ৯৭২
(খ) ৪০৫৬
(গ) ২১৯৫২

৫। ৪৬৩৯ থেকে কোন ক্ষুদ্রতম সংখ্যা বিয়োগ করলে বিয়োগফল একটি পূর্ণ বর্গসংখ্যা হবে?

৬। ৫৬০৫ এর সাথে কোন ক্ষুদ্রতম সংখ্যা যোগ করলে যোগফল একটি পূর্ণ বর্গসংখ্যা হবে?

পূর্ণসংখ্যা বা অখণ্ড সংখ্যার বর্গমূল ভাগের সাহায্যে যেভাবে নির্ণয় করা হয়েছে, দশমিক ভগ্নাংশের বর্গমূলও সেই নিয়মেই নির্ণয় করা হয়। দশমিক ভগ্নাংশের দুটি অংশ থাকে। দশমিক বিন্দুর বামদিকের অংশকে অখণ্ড বা পূর্ণ অংশ এবং দশমিক বিন্দুর ডানপাশের অংশকে দশমিক অংশ বলা হয়।

বর্গমূল করার নিয়ম

• অখণ্ড অংশে একক থেকে ক্রমান্বয়ে বামদিকে প্রতি দুই অঙ্কের উপর দাগ দিতে হয়।
• দশমিক অংশে দশমিক বিন্দুর ডানপাশের অঙ্ক থেকে শুরু করে ডানদিকে ক্রমান্বয়ে জোড়ায় জোড়ায় দাগ দিতে হয়। এরূপে যদি দেখা যায় সর্বশেষে মাত্র একটি অঙ্ক বাকি আছে, তবে তারপরে একটি শূন্য বসিয়ে দুই অঙ্কের উপর দাগ দিতে হয়।
• সাধারণ নিয়মে বর্গমূল নির্ণয়ের প্রক্রিয়ায় অখণ্ড অংশের কাজ শেষ করে দশমিক বিন্দুর পরের প্রথম দুটি অঙ্ক নামানোর আগেই বর্গমূলে দশমিক বিন্দু দিতে হয়।
• দশমিক বিন্দুর এক জোড়া শূন্যের জন্য বর্গমূলে দশমিক বিন্দুর পর একটি শূন্য দিতে হয়।

উদাহরণ ১। ২৬.৫২২৫ এর বর্গমূল নির্ণয় কর।

সমাধান:

নির্ণেয় বর্গমূল = ৫.১৫

উদাহরণ ২। ০.০০২৯১৬ এর বর্গমূল নির্ণয় কর।

সমাধান:

নির্ণেয় বর্গমূল = ০.০৫৪

বর্গমূলের আসন্ন মান নির্ণয়

তিন দশমিক স্থান পর্যন্ত বর্গমূল নির্ণয় করতে হলে, সংখ্যার দশমিক বিন্দুর পর কমপক্ষে ৬টি অঙ্ক নিতে হয়। দরকার হলে ডানদিকের শেষ অঙ্কের পর প্রয়োজনমতো শূন্য বসাতে হয়। এতে সংখ্যার মানের পরিবর্তন হয় না।

উদাহরণ ৩। ৯.২৫৩ এর বর্গমূল তিন দশমিক স্থান পর্যন্ত আসন্ন মান নির্ণয় কর।

সমাধান:

নির্ণেয় বর্গমূল = ৩.০৪২ (প্রায়)

উদাহরণ ৪। ১২৩ এর বর্গমূল দুই দশমিক স্থান পর্যন্ত নির্ণয় কর।

সমাধান:

নির্ণেয় বর্গমূল = ১১.০৯০ (প্রায়)

দ্রষ্টব্য: উপরের বর্গমূলে দশমিকের পর চতুর্থ অঙ্কটি ৮ হওয়ায় তৃতীয় অঙ্কটির সাথে ১ যোগ করে নির্ণেয় বর্গমূলের (তিন দশমিক স্থান পর্যন্ত আসন্ন মান হল ৩.০৪২।

• দুই দশমিক স্থান পর্যন্ত বর্গমূল নির্ণয় করতে হলে, তিন দশমিক স্থান পর্যন্ত বর্গমূল নির্ণয় করতে হবে।
• বর্গমূলে যত দশমিক স্থান পর্যন্ত নির্ণয় করতে হবে এর পরের অঙ্কটি ০, ১, ২, ৩ বা ৪ হলে পূর্বের অঙ্কের সাথে ১ যোগ হবে না।
• বর্গমূলে যত দশমিক স্থান পর্যন্ত নির্ণয় করতে হবে এর পরের অঙ্কটি ৫, ৬, ৭, ৮ বা ৯ হলে পূর্বের অঙ্কের সাথে ১ যোগ হবে।

$\frac{৫০ }{৩২}$ কে লঘিষ্ঠ আকারে লিখে পাই $\frac{২৫ }{১৬}$

এখানে $\frac{২৫ }{১৬}$ ভগ্নাংশের লব ২৫ একটি পূর্ণ বর্গসংখ্যা এবং হর ১৬ একটি পূর্ণ বর্গসংখ্যা। সুতরাং $\frac{২৫ }{১৬}$ একটি পূর্ণবর্গ ভগ্নাংশ।

কোনো ভগ্নাংশের লব ও হর পূর্ণ বর্গসংখ্যা বা ভগ্নাংশকে লঘিষ্ঠ আকারে পরিণত করলে যদি তার লব ও হর পূর্ণ বর্গসংখ্যা হয়, তবে ঐ ভগ্নাংশকে পূর্ণবর্গ ভগ্নাংশ বলা হয়।

ভগ্নাংশের লবের বর্গমূলকে হরের বর্গমূল দ্বারা ভাগ করলে ভগ্নাংশের বর্গমূল পাওয়া যায়।

উদাহরণ ৫। $\frac{৬৪ }{৮১}$ এর বর্গমূল নির্ণয় কর।

সমাধান: ভগ্নাংশটির লব ৬৪ এর বর্গমূল = $\sqrt{৬৪}$ =৮

এবং হর ৮১ এর বর্গমূল = $\sqrt{৮১}$ = ৯

$\frac{৬৪ }{৮১}$ এর বর্গমূল $\sqrt{\frac{৬৪ }{৮১}} \frac{৮}{৯}$

নির্ণেয় বর্গমূল $\frac{৮}{৯}$

উদাহরণ ৬। $৫২\frac{৯}{১৬}$ এর বর্গমূল নির্ণয় কর।

সমাধান: $৫২\frac{৯}{১৬}$ এর বর্গমূল $\sqrt{৫২\frac{৯}{১৬}}=\sqrt{\frac{৮৪১}{১৬}}=\frac{২৯}{৪}=৭\frac{১}{৪}$

$৫২\frac{৯}{১৬}$ এর বর্গমূল $৭\frac{১}{৪}$

ভগ্নাংশের হর যদি পূর্ণ বর্গসংখ্যা না হয়, তবে গুণন দ্বারা একে পূর্ণবর্গ করে নিতে হয়।

উদাহরণ ৭। $২\frac{৮}{১৫}$ এর বর্গমূল তিন দশমিক স্থান পর্যন্ত নির্ণয় কর।

সমাধান:

$২\frac{৮}{১৫}$এর বর্গমূল

$$\begin{gathered} =\sqrt{ ২\frac{৮}{১৫}} \\ = \sqrt{\frac{৩৮}{১৫}} \\ =\sqrt{\frac{৩৮\times ১৫}{১৫\times ১৫}} \\ =\sqrt{\frac{৫৭০}{২২৫}} \\ =\frac{২৩.৮৭৪৭}{১৫ } \\ =১.৫৯১৬ \end{gathered}$$

আসন্ন তিন দশমিক স্থান পর্যন্ত বর্গমূল = ১.৫৯১৬ (প্রায়)

১,২,৩,৪, _______ ইত্যাদি স্বাভাবিক সংখ্যা। সংখ্যাগুলোকে দুটি স্বাভাবিক সংখ্যার ভগ্নাংশ আকারে নিম্নরূপে লেখা যায়।

$১=\frac{১}{১}, ২=\frac{২}{১},৩=\frac{৩\times ২}{২}=\frac{৬}{২},$ _____________ ইত্যাদি।

আবার, ০.১, ১.৫, ২.০৩, _______ ইত্যাদি দশমিক সংখ্যা।

এখানে $০.১ = \frac{১}{১০}, ১.৫ = \frac{১৫}{১০}, ২.৩০ =\frac{২০৩}{১০০}$ যা সংখ্যাগুলোর ভগ্নাংশ আকার।

আবার $০\frac{০}{১}$ একটি ভগ্নাংশ সংখ্যা।

উপরে বর্ণিত সংখ্যাগুলো মূলদ সংখ্যা।
অতএব, শূন্য, সকল স্বাভাবিক সংখ্যা ও ভগ্নাংশ সংখ্যা মূলদ সংখ্যা।

অমূলদ সংখ্যা: $\sqrt{২}== ১.৪১৪২১৩৫$ _______ সংখ্যার দশমিকের পরে অঙ্ক সংখ্যা নির্দিষ্ট নয়। ফলে দুটি স্বাভাবিক সংখ্যার ভগ্নাংশ আকারে লেখা যায় না। অনুরূপে $\sqrt{৩},\sqrt{৫},\sqrt{৭}$ _______ ইত্যাদি । সংখ্যাগুলোকে ও দুটি স্বাভাবিক সংখ্যার ভগ্নাংশ আকারে প্রকাশ করা যায় না। তাই এগুলো অমূলদ সংখ্যা।

লক্ষ করি: $\sqrt{২},\sqrt{৩},\sqrt{৫},\sqrt{৬}$ _________ ইত্যাদি অমূলদ সংখ্যা এবং ২,৩,৫,৬ _________ ইত্যাদি পূর্ণ বর্গসংখ্যা নয়। সুতরাং পূর্ণ বর্গসংখ্যা নয় এরূপ সংখ্যার বর্গমূল অমূলদ সংখ্যা।

উদাহরণ ৮। ০.১২ $\sqrt{২৫},\sqrt{৭২},\frac{\sqrt{৪৯}}{৭}$ সংখ্যাগুলো থেকে অমূলদ সংখ্যা বাছাই কর।

সমাধান: এখানে,

$\sqrt{২৫}=\sqrt{{৫}^{২}}=$ ৫ যা একটি স্বাভাবিক সংখ্যা $\sqrt{৭২}=\sqrt{২\times ৩৬}=\sqrt{২\times {৬}^{২}}=৬\sqrt{২}$ যা ভগ্নাংশ আকারে লেখা যায় না।

এবং $\frac{\sqrt{৪৯}}{৭}=\frac{\sqrt{{৭}^{২}}}{৭}=\frac{৭}{৭}$ = ১ ; যা একটি স্বাভাবিক সংখ্যা।

$০.১২ , \sqrt{২৫},\frac{\sqrt{৪৯}}{৭}$ মূলদ সংখ্যা এবং $\sqrt{৭২}$ অমূলদ সংখ্যা।

সংখ্যারেখার মূলদ সংখ্যা

নিচের সংখ্যারেখাটি লক্ষ করি:

উপরের সংখ্যারেখাটিতে গাঢ় চিহ্নিত বৃত্তটি ২ এর অবস্থান নির্দেশ করে।

আবার,

উপরের সংখ্যারেখাটিতে গাঢ় চিহ্নিত বৃত্তটির অবস্থান ১ ও ২ এর মাঝে। গাঢ় চিহ্নিত অংশটুকু ৪ ভাগের $১+\frac{৩}{৪}$ বা $১\frac{৩}{৪}$ নির্দেশ করে।

সংখ্যারেখায় অমূলদ সংখ্যা

$\sqrt{৩}$ একটি অমূলদ সংখ্যা যেখানে $\sqrt{৩} = ১.৭৩২$ __________ = ১.৭ (আসন্ন মান)।

এবার সংখ্যারেখায় ১ ও ২ এর মাঝের অংশকে সমান ১০ অংশে ভাগ করে সপ্তম অংশটি গাঢ় করি যার আসন্ন মান ১.৭ তথা $\sqrt{৩}$ নির্দেশ করে।

অতএব গাঢ় চিহ্নিত বৃত্তটি সংখ্যারেখায় $\sqrt{৩}$ অবস্থান।

উদাহরণ ৯। কোনো বাগানে ১২৯৬টি আমগাছ আছে। বাগানের দৈর্ঘ্য ও প্রস্থের উভয় দিকের প্রত্যেক সারিতে সমান সংখ্যক আমগাছ থাকলে প্রত্যেক সারিতে গাছের সংখ্যা নির্ণয় কর।

সমাধান: বাগানের দৈর্ঘ্য ও প্রস্থের উভয় দিকের প্রত্যেক সারিতে সমান সংখ্যক আমগাছ আছে।

প্রত্যেক সারিতে আমগাছের সংখ্যা হবে ১২৯৬ এর বর্গমূল।

এখন,

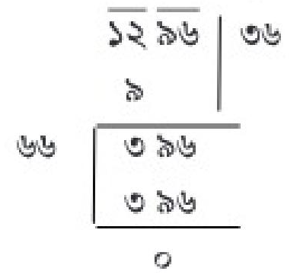
নির্ণেয় আমগাছের সংখ্যা ৩৬ টি।

উদাহরণ ১০। একটি স্কাউট দলকে ৯, ১০, এবং ১২ সারিতে সাজানো যায়। আবার তাদের বর্গাকারেও সাজানো যায়। ঐ স্কাউট দলে কমপক্ষে কতজন স্কাউট রয়েছে?

সমাধান: স্কাউট দলকে ৯, ১০ এবং ১২ সারিতে সাজানো যায়। ফলে স্কাউট এর সংখ্যা ৯, ১০ এবং ১২ দ্বারা বিভাজ্য। এরূপ ক্ষুদ্রতম সংখ্যা হবে ৯, ১০ এবং ১২ এর ল.সা.গু.।

এখানে,

৯, ১০ এবং ১২ এর ল.সা.গু. $২ \times ২ \times ৩\times ৩\times ৫ = (২ \times ২) \times (৩ \times ৩) \times ৫$

প্রাপ্ত ল.সা.গু. $(২ \times ২) \times (৩\times ৩) \times ৫$ কে বর্গাকারে সাজানো যায় না।

$(২ \times ২) \times (৩ \times ৩) \times ৫$ কে বর্গসংখ্যা করতে হলে কমপক্ষে ৫ দ্বারা গুণ করতে হবে।

৯, ১০ এবং ১২ সারিতে এবং বর্গাকারে সাজানোর জন্য স্কাউট এর সংখ্যা প্রয়োজন $(২ \times ২) \times (৩ \times ৩) \times (৫ \times ৫) = ৯০০$

নির্ণেয় স্কাউট এর সংখ্যা ৯০০।

উদাহরণ ১১। ২১৯৫২ এবং ৫৬০৫ দুটি সংখ্যা।

(ক) প্রথম সংখ্যাটি কী পূর্ণবর্গ সংখ্যা যুক্তি দাও।
(খ) প্রথম সংখ্যাটি যদি পূর্ণবর্গ না হয়, তবে একে কোন ক্ষুদ্রতম সংখ্যা দ্বারা ভাগ করলে পূর্ণবর্গ সংখ্যা হবে।
(গ) দ্বিতীয় সংখ্যাটির সাথে কোন ক্ষুদ্রতম সংখ্যা যোগ করলে, যোগফল একটি পূর্ণবর্গ সংখ্যা হবে।

সমাধান:

(ক) যে সংখ্যার সর্ব ডানদিকের অঙ্ক অর্থাৎ একক স্থানীয় অঙ্ক ২ বা ৩ বা ৭ বা ৮ তা পূর্ণবর্গ নয়। যেহেতু ২১৯৫২ সংখ্যাটির একক স্থানীয় অঙ্কটি ২ সেহেতু সংখ্যাটি পূর্ণবর্গ নয়।

(খ)
এখানে

সুতরাং $২১৯৫২= ২\times ২\times ২\times ২\times ২\times ২\times ৭\times ৭\times ৭$

২১৯৫২ সংখ্যাটি পূর্ণবর্গ নয়। সংখ্যাটিকে ৭ দ্বারা ভাগ করলে প্রাপ্ত সংখ্যাটি পূর্ণবর্গ হবে।
উত্তর: ৭

গ. এখানে,

যেহেতু সংখ্যাটির বর্গমূল নির্ণয় করার সময় ভাগশেষ ১২৯ আছে সেহেতু সংখ্যাটি পূর্ণবর্গ নয়। ৫৬০৫ এর সাথে কোনো একটি ক্ষুদ্রতম সংখ্যা যোগ করলে যোগফল পূর্ণবর্গ হবে।

বর্গমূল হবে (৭৪+১)=৭৫

৭৫ এর বর্গ = (৭৫ $\times$ ৭৫)=৫৬২৫

সুতরাং, নির্ণেয় ক্ষুদ্রতম সংখ্যাটি=৫৬২৫-৫৬০৫=২০

উত্তর: ২০

১। $\frac{২৮৯ }{৩৬১}$ এর বর্গমূল কত?

(ক) $\frac{১৩ }{১৯}$

(খ) $\frac{১৭}{১৯}$

(গ) $\frac{১৯ }{১৩}$

(ঘ) $\frac{১৯ }{১৭}$

২। ১.১০২৫ এর বর্গমূল কত?

(ক) ১.৫
(খ) ১.০০৫
(গ) ১.০৫
(ঘ) ০.০৫

৩। একটি মূলদ সংখ্যা হলো-
(i) ০
(ii) ৫
(iii) $\frac{৫}{২}$
নিচের কোনটি সঠিক?

(ক) i ও ii
(খ) i ও iii
(গ) ii ও iii
(ঘ) i, ii ও iii

দুটি ক্রমিক সংখ্যার বর্গের অন্তর ১৯।
এই তথ্য থেকে ৪ ও ৫ নং প্রশ্নের উত্তর দাও।

8।একটি সংখ্যা ১০ হলে অপরটি কত?

(ক) ১২
(খ) ১১
(গ) ৯
(ঘ) ৮

৫। সংখ্যা দুটির বর্গের যোগফল কত?

(ক) ২৮১
(খ) ২২১
(গ) ১৮১
(ঘ) ১৬৪

৬। ০.০১ এর বর্গমূল নিচের কোনটি?

(ক) ০.০১
(খ) ০.১
(গ) ০.০০১
(ঘ) ০.০০০১

৭। কোনো সংখ্যার একক স্থানীয় অংক ২ বা ৮ হলে তার বর্গসংখ্যার একক স্থানীয় অঙ্কটি হবে-

(ক) ২
(খ) 8
(গ) ৬
(ঘ) ৮

৮। $৩\times ৭\times ৫\times ৭\times ৩$ কে কত দ্বারা গুণ বা ভাগ করলে পূর্ণ বর্গসংখ্যা হবে?

(ক) ৩
(খ) ৫
(গ) ৭
(ঘ) ১১

৯। নিচের কোনটি অমূলদ সংখ্যা

(ক) $\sqrt{২}$
(খ) $\sqrt{৯}$
(গ) $\sqrt{১৬}$
(ঘ)$\sqrt{২৫}$

১০। একজন কৃষক বাগান করার জন্য ৫৯৫টি চারাগাছ কিনে আনেন। প্রত্যেকটি চারাগাছের মূল্য ১২ টাকা।

(ক) চারাগাছগুলো কিনতে তাঁর কত খরচ হয়েছে?
(খ) বাগানে প্রত্যেক সারিতে সমান সংখ্যক গাছ লাগানোর পর কয়টি চারাগাছ অবশিষ্ট থাকবে?
(গ) খরচের টাকার সংখ্যা ও চারাগাছের সংখ্যার বিয়োগফলের সাথে কোন ক্ষুদ্রতম সংখ্যা যোগ করলে যোগফল একটি পূর্ণ বর্গসংখ্যা হবে?

১১। বর্গমূল নির্ণয় কর।

(ক) ০.৩৬
(খ) ২.২৫
(গ) ০.০০৪৯
(ঘ) ৬৪১.১০২৪
(ঙ) ০.০০০৫৭৬
(চ) ১৪৪.৮৪১২২৫

১২। দুই দশমিক স্থান পর্যন্ত বর্গমূল নির্ণয় কর।

(ক) ৭
(খ) ২৩.২৪
(গ) ০.০৩৬

১৩। নিচের ভগ্নাংশগুলোর বর্গমূল নির্ণয় কর।

(ক) $\frac{১}{৬৪}$
(খ) $\frac{৪৯}{১২১}$
(গ) $১১\frac{৯৭}{১৪৪}$
(ঘ) $৩২\frac{২৪১}{৩২৪}$

১৪। তিন দশমিক স্থান পর্যন্ত বর্গমূল নির্ণয় কর।

(ক) $\frac{৬}{৭}$
(খ) $২\frac{৫}{৬}$
(গ) $৭\frac{৯}{১৩}$

১৫। ৫৬৭২৮জন সৈন্য থেকে কমপক্ষে কতজন সৈন্য সরিয়ে রাখলে বা তাদের সাথে কমপক্ষে আর কতজন সৈন্য যোগ দিলে সৈন্যদলকে বর্গাকারে সাজানো যাবে?

১৬। কোনো বিদ্যালয়ের ২৭০৪জন শিক্ষার্থীকে প্রাত্যহিক সমাবেশ করার জন্য বর্গাকারে সাজানো হলো। প্রত্যেক সারিতে শিক্ষার্থীর সংখ্যা নির্ণয় কর।

১৭। একটি সমবায় সমিতির যতজন সদস্য ছিল প্রত্যেকে তত ২০ টাকা করে চাঁদা দেওয়ায় মোট ২০৪৮০ টাকা হলো। ঐ সমিতির সদস্য সংখ্যা নির্ণয় কর।

১৮। কোনো বাগানে ১৮০০ টি চারাগাছ বর্গাকারে লাগাতে গিয়ে ৩৬টি গাছ বেশি হলো। প্রত্যেক সারিতে চারাগাছের সংখ্যা নির্ণয় কর।

১৯। কোন ক্ষুদ্রতম পূর্ণ বর্গসংখ্যা ৯, ১৫ এবং ২৫ দ্বারা বিভাজ্য?

২০। একটি ধানক্ষেতের ধান কাটতে শ্রমিক নেওয়া হলো। প্রত্যেক শ্রমিকের দৈনিক মজুরি তাদের সংখ্যার ১০ গুণ। দৈনিক মোট মজুরি ৬২৫০ টাকা হলে শ্রমিকের সংখ্যা বের কর।

২১। দুটি ক্রমিক সংখ্যার বর্গের অন্তর ৩৭ হলে, সংখ্যা দুটি নির্ণয় কর।

২২। এমন দুটি ক্ষুদ্রতম ক্রমিক সংখ্যা নির্ণয় কর যাদের বর্গের অন্তর একটি পূর্ণ বর্গসংখ্যা।